what is the solution to the following system of equations 3x+2y+z=7

Key Questions

• An augmented matrix contains the coefficients of the unknowns and the "pure" coefficients. Y'all can manipulate the rows of this matrix (elementary row operations) to transform the coefficients and to "read", at the end, the solutions of your system.

  The 2 row operations allowed are:
  1) swap rows;
  ii) take the elements of a row, multiply them by a scalar and sum them to the respective element of another row.

  I show you an example. Let us have the following system:
  
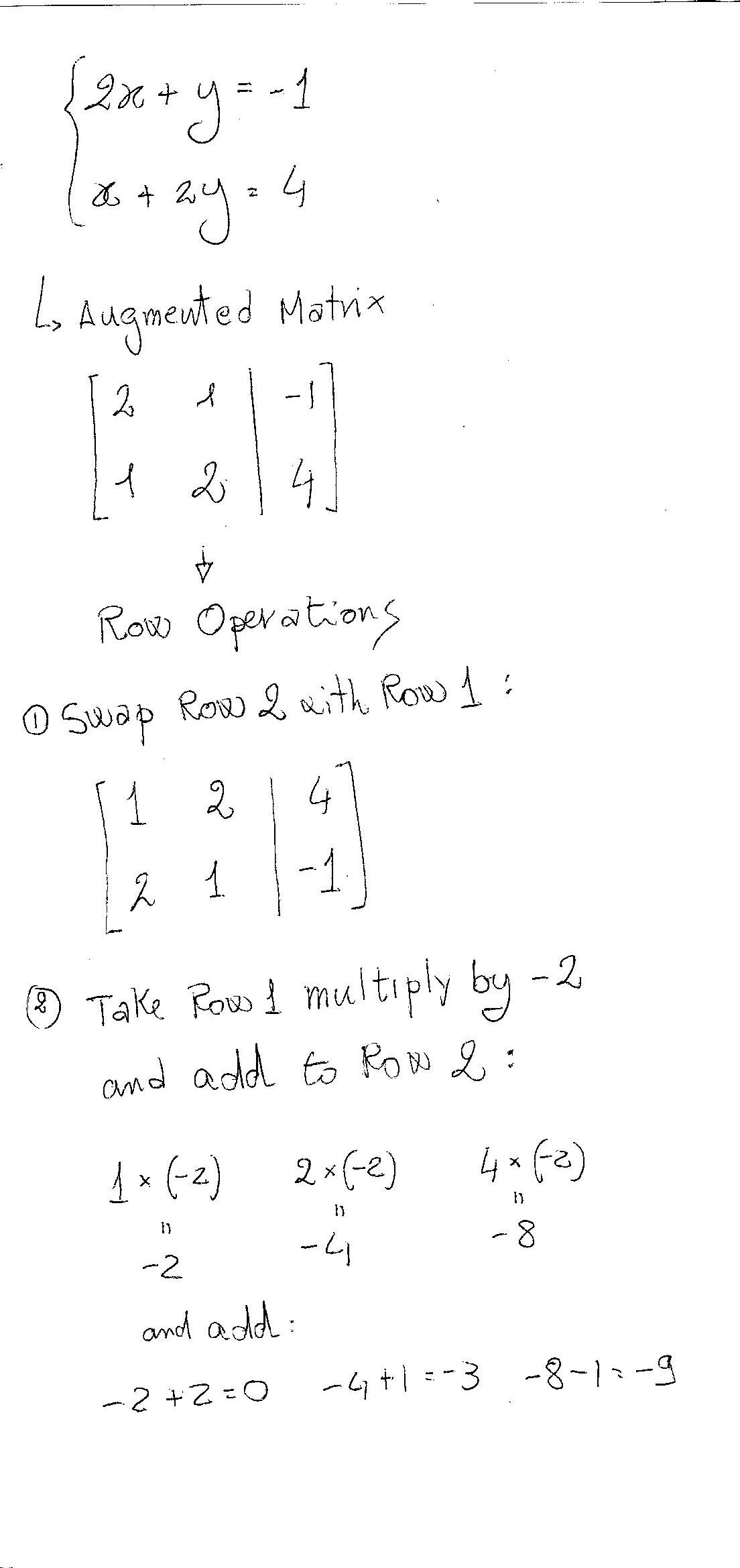
  Yous can see that now Row 2 contains a zilch. This is good because you eliminate 1 unknown from the equation represented by Row two and so yous can "run across" the value of the remaining one.
  

  You can now apply the same idea to bigger systems with more equations and unknowns.

• Consider a normal equation in #x# such as:
  #3x=half-dozen#
  To solve this equation you only take the #3# in front end of #ten# and put it, dividing, below the #6# on the correct side of the equal sign.
  #x=6/3=iii^-ane*6=2#
  at this indicate yous can "read" the solution equally: #x=2#.
  With a arrangement of #north# equations in #n# unknowns you do basically the aforementioned, the only difference is that you have more than i unknown (and equation) that can now be represented by matrices and by the inverse matrix in place of the coefficient to the -one (in our instance is #3^-one#).

  You can utilize matrices and alter your system in a matrix equation :
  If yous take the post-obit system:
  
  (where #a,b,c,d,east,g# are real numbers)
  you lot tin can change it in a matrix equation:
  
  Where #A# is the matrix of the coefficients of the unknowns, #U# is the column of the unknown and #B# is the column of the pure coefficients (without unknowns).

  You can check that this representation with matrices represents the organization by doing the multiplication #A*U# and setting it equal to #B# you'll get back your original system!!!

  At present, to solve your matrix equation #A*U=B# y'all can multiply both sides by the inverse of #A#, i.east. #A^-i#
  
  (Remembering that #I# is the identity matrix .

  For example:
  
  And then:
  #ten=-3#
  #y=5#

• I would employ Cramer'south Rule .
  This rule is based upon using the matrix associated with the coefficients of the unknowns and of the pure coefficients of your organization, evaluate their determinants and combine them to evaluate the values of the unknowns.

  Consider an case:

  

  Now we consider iii other matrices, #A_x, A_y and A_z# and their determinant. These matrices are obtained by substituting each column of #A# with the column of pure coefficients (the ones without unknown):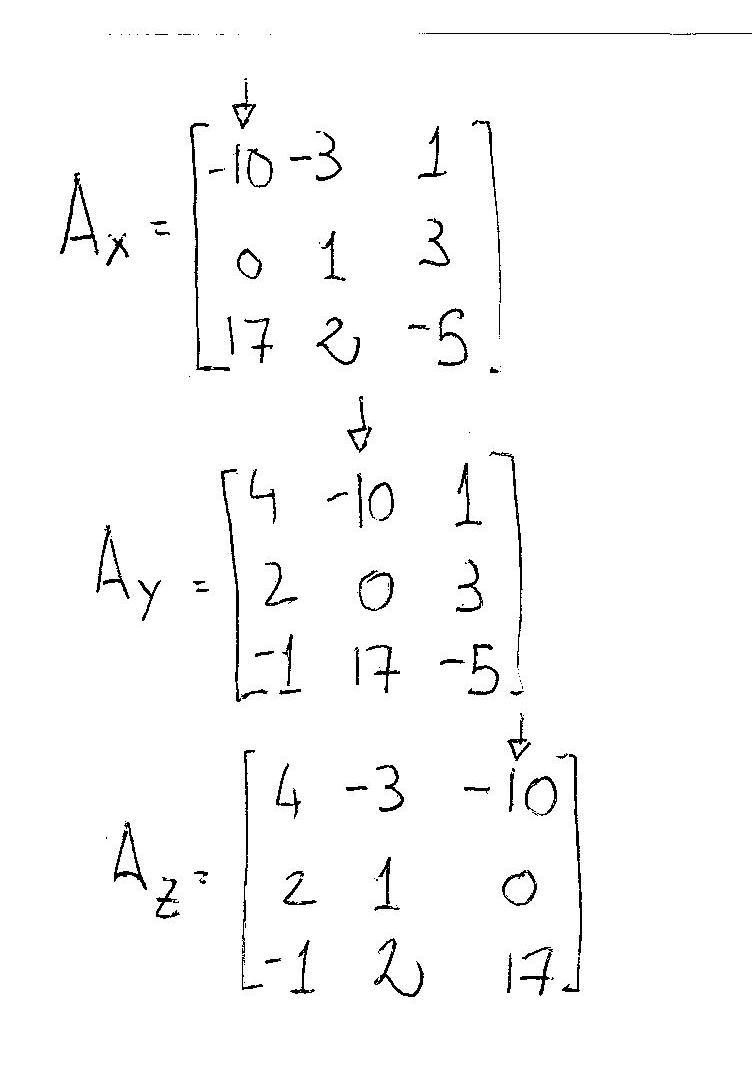

  

  We evaluate the three determinants for these matrices:

  

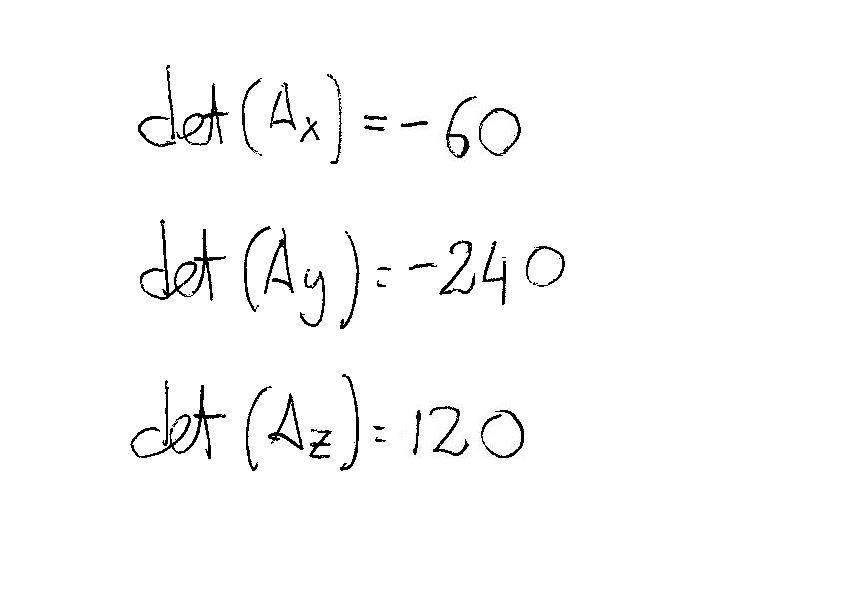
  Finally nosotros tin can calculate the values of the unknowns every bit:

  #x=det(A_x)/(det(A))=(-threescore)/-60=ane#
  #y=det(A_y)/(det(A))=(-240)/-threescore=four#
  #z=det(A_z)/(det(A))=(120)/-60=-2#

  Your final outcome is:
  #x=one#
  #y=4#
  #z=-ii#

• You tin solve a square arrangement of ii linear equations using Cramer's Rule or Reduced Row Echelon Form.

  A foursquare system has the same number of equations every bit variables. A foursquare system can be classified as independent, dependent, or inconsistent.

  If you accept more variables than equations, you would have an underdetermined organization and will be classified as dependent or inconsistent.

  If you have fewer variables than equations, yous would have an overdetermined system and will be classified every bit independent, dependent, or inconsistent. Withal in the instance of just 2 equations, it cannot be dependent.

  Reduced Row Echelon Form (RREF) is solving the arrangement similar to using the elimination method to solve a organisation of linear equations.

  Cramer's Dominion is solving the system using determinants. Cramer's Rule is non necessarily faster than RREF, but it doesn't require thinking considering information technology is a formula; this is skilful for calculators and computers.

  Solving with a matrix is usually quicker than solving with variables because there is less to write out. Furthermore, we have other techniques to solve the system over elimination and substitution.

  So search for RREF and Cramer'southward Rule equally at that place are plenty of examples available.

• How do you solve #2x+A=B# given #A=((2, -8), (9, 5), (-2, 3))# and #B=((-6,two), (i, -5), (eight, 5))#?

• How do you solve #Ax=B# given #A=((two, 0, 0), (-1, 2, 0), (-2, iv, 1))# and #B=((four), (10), (11))#?

• How do you lot solve #3x+A=B# given #A=((-3, -7), (2, -9), (5, 0))# and #B=((-5, -i), (0, 0), (iii, -iv))#?

• How do yous solve #((one, -6, 0), (0, 1, -7), (3, 0, ii))X=((ane), (4), (11))#?

• How do you solve #((ii, 2, 0), (4, -iii, two), (0, -3, 5))x=((-10), (two), (-9))#?

• How do you lot solve #((2, 0, 0), (-ane, 2, 0), (-2, iv, one))10=((4), (ten), (11))#?

• How do you solve #((five, i, 4), (2, -3, -4), (vii, two, -six))X=((5), (2), (five))#?

• How exercise you multiply three matrices given #((-1, four, -2, 0), (3, 3, 1, -4), (0, five, 2, -1))# and #((1, 2, 5), (-3, iv, 0), (ii, 3, -4), (-1, 2, 2))# and #((-2), (4), (3))#?

• How do you lot solve #[(-x,+2y,-4z,-5u,=,27),(-2x,-3y,+3z,-3u,=,9),(5x,-4y,+2z,-3u,=,5), (-2x,+0y,+4z,-5u,=,29)]#?

• How do you solve #[(1,-2,3), (ii,-4,vi), (3,-half-dozen,9)][(x), (y), (z)]=[(0),(0),(0)]#?

davissatedilly.blogspot.com

Source: https://socratic.org/precalculus/matrix-row-operations/solving-a-system-of-equations-using-a-matrix

Share this post